伽利略变换式可用哪些方面

伽利略变换式可用哪些方面

伽利略变换(Galilean transformation)是牛顿力学中所使用的两个相对做等速直线运动的参考系中的时空变换， 属于一种被动态变换。伽利略变换中，直观上明显成立的公式在物体以接近光速运动时就会瓦解，这是相对论性效应造成的。

伽利略变换建基于人们加减物体速度的直觉，变换的核心是假设时间、空间是绝对的、彼此独立的，其中时间均匀流逝，空间均匀分布且各向同性。

基本信息

中文名称

伽利略变换

外文名称

Galilean transformation

力学

牛顿力学

算法

公式

属性

概念

目录

1平移变换

2三种伽利略变换

3变换的局限

折叠编辑本段平移变换

伽利略变换是整个经典力学的支柱。该理论认为空间是独立的，与在其中物体的运动无关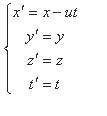，而时间是均匀流逝的，线性的。

请点击输入图片描述

伽利略变换的数学表达式(如右图)。

伽利略变换是牛顿力学中所使用的两个相对做等速直线运动的参考系中的时空变换。设有两个参考系S(Oxyz)及S'(O'x'y'z')，坐标轴相互平行且轴x与轴x'重合，S'相对S沿x轴以u做等速直线运动，且S系与S'系中各处有结构完全相同的时钟，记录的时刻为t与t'，并以两坐标原点O及O'重合时刻为计时起点，则可得某质点m的运动在两参考系中的时空变换关系:

伽利略

请点击输入图片描述

x'=x-ut y'=y z'=z t'=t

上式即为伽利略(坐标)变换。最后一条方程式意味着时间是不受观测者的相对运动影响的。

如果将各式对时间求导，则得速度变换式:

vx'=vx-u vy'=vy vz'=vz

因此，如果S是惯性系，即不受外力作用的物体在其中做等速直线运动，则根据上式，它在S'中也一定做等速直线运动，所以S'也是惯性系。如果将各式再一次对时间求导，则得加速度变换关系式:

ax'=ax ay'=ay az'=az

亦即a'=a。因此如果S是惯性系，即在其中F=ma成立，则在S'中也有F=ma'，所以S'也是惯性系。这样就从伽利略变换导出了力学相对性原理。

利用线性代数的术语来说，这种变换是个错切，是矩阵对向量进行变换的一个过程。

折叠编辑本段三种伽利略变换

伽利略变换可以唯一写成由时空的旋转、平移和均速运动复合而成的函数。设x为三维空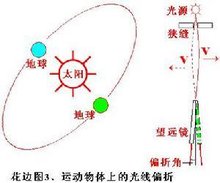运动物体上的光线也发生了弯曲间中的一点，t为一维时间中的一点。时空当中的任何一点可以表达为有序对(x,t)。速度为v的均速运动表达为:

请点击输入图片描述

(X，t)→(X+tv，t)，其中v在R内。

平移表达为:

(X，t)→(X+a，t+b)，其中a在R内，b在R内。

旋转表达为:

(X，t)→(GX，t)，其中G:R → R为某正交变换。作为一个李群，伽利略变换的维度为10。

折叠编辑本段变换的局限

伽利略变换与牛顿的绝对时间、绝对空间的概念有关。这里所谓绝对是指长度的量度与时间的量度均与参考系的运动或参考系的选择无关。现代物理学中，电、磁、光学现象所符合的相对性原理与伽利略变换发生了尖锐的矛盾，因此在狭义相对论中修改了绝对时空的概念，空间和时间遵从洛伦兹变换。这时长度与时间的量度都与参考系的速度有关。不过在运动速度远小于光的速度时，洛伦兹变换近似等于伽利略变换 。